Lenticular Poster Printing Lenses
Lenticular Printing resembles both a science and an art in that it takes great precision to produce spectacular lenticular images. In order to create the perfect 3D Poster, 3D In-Store Displays, 3D POP displays, or other form of promotional material, it's necessary to match the right LPI - lines per inch - with the onlooker's viewing angle and viewing distance, while considering exactly which type of optical effect you're looking to accomplish. Before you can familiarize yourself with the type of lenticular you'd like to order, it might be helpful to clarify a few of these terms:
LPI - As mentioned on our What is Lenticular? page, lenticular lenses are lined with a series ridges, tiny lenses called lenticules. The LPI is the number of lenticules per inch on a lens. Generally speaking, the smaller the LPI, the farther the viewing distance. This will become important as you decide on what type of effect you'd like to achieve and the product size you're hoping to print.
Viewing Distance - The viewing distance is how far away you anticipate your onlookers to be. Are you trying to get the attention of someone across the street with a 3D movie poster? Or are you handing out image-morphing Lenticular Posters at a trade show?
Viewing Angle - This is the optimal angle at which customers will need to look at your lenticular. A large 3D poster will most likely be seen head on at an angle of 18 degrees. A flipping poster will be held in their hand, so you'd probably want them to look down at it at a 48 degree angle.
Below, we have a helpful table of viewing distances, viewing angles, and effects as they correspond with the LPI and size of the image you'd like to create. Also included is the type of material used to make the various lenticulars, their thickness, and weight.
Lenticular Lens Specs
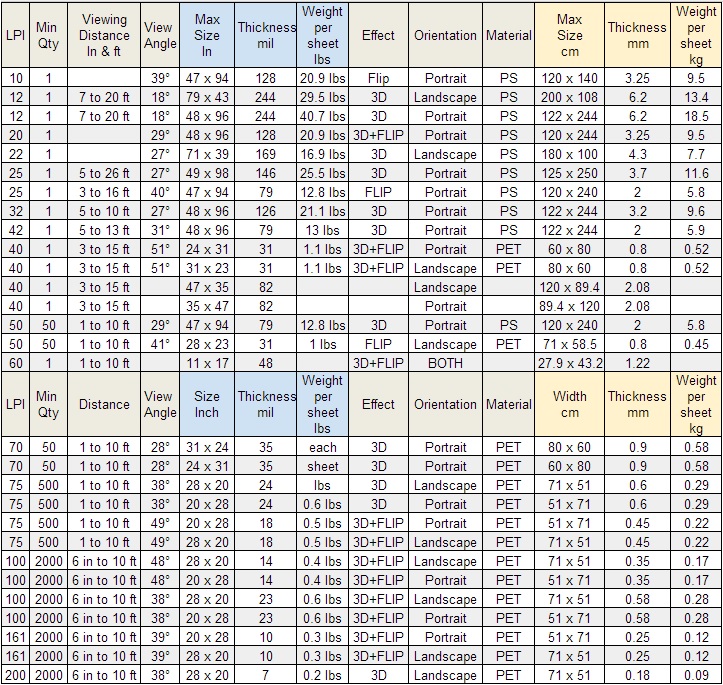
** What is the viewing angles of Lenticular with 3D Depth effect?
The smaller the degree of the viewing angle, the larger the viewing distance for 3D.
|
